グラフを利用して高次不等式を簡単に解く方法

3次以上の不等式を高次不等式といいます．

この記事では，多項式関数のグラフの特徴を利用して高次不等式を簡単に解く方法を解説します．

因数定理を使った因数分解

高次不等式を解く際は，整理した式をまず因数分解します．

因数分解には因数定理を用います．

高次式の因数分解の解説は下記を参照してください．

組立除法を使わずに高次式を因数分解する方法

多項式関数のグラフの特徴

高次不等式を簡単に解くために必要な多項式関数のグラフの特徴を説明します．

その特徴は以下の通りです．

$n$ が偶数のとき，
最高次の係数が正である $n$ 次関数のグラフは左から見て...

• 右下がりで始まる
• 右上がりで終わる

$n$ が奇数のとき，
最高次の係数が正である $n$ 次関数のグラフは左から見て...

• 右上がりで始まる
• 右上がりで終わる

ここから，2次関数から5次関数までの具体的な特徴を説明します．

2次関数のグラフ

2次関数 $y = ax^2 + bx + c$ （$a \neq 0$，$b$，$c$ は任意）において，
$a \gt 0$ のときのグラフは左から見て...

• 右下がりで始まる
• 右上がりで終わる

3次関数のグラフ

3次関数 $y = ax^3 + bx^2 + cx + d$ （$a \neq 0$，$b$，$c$，$d$ は任意）において，
$a \gt 0$ のときのグラフは左から見て...

• 右上がりで始まる
• 右上がりで終わる

4次関数のグラフ

4次関数 $y = ax^4 + bx^3 + cx^2 + dx + e$ （$a \neq 0$，$b$，$c$，$d$，$e$ は任意）において，
$a \gt 0$ のときのグラフは左から見て...

• 右下がりで始まる
• 右上がりで終わる

5次関数のグラフ

5次関数 $y = ax^5 + bx^4 + cx^3 + dx^2 + ex + f$ （$a \neq 0$，$b$，$c$，$d$，$e$，$f$ は任意）において，
$a \gt 0$ のときのグラフは左から見て...

• 右上がりで始まる
• 右上がりで終わる

例題と解説

例1　不等式 $x^3 - 3x^2 + 2x > 0$ を解け．

まず，左辺を因数分解します．

$\begin{eqnarray*} x^3 - 3x^2 + 2x > 0\\ x(x^2 -3x +2) \gt 0\\ x(x-1)(x-2) \gt 0 \end{eqnarray*}$


次に，多項式関数のグラフの特徴を利用して，
$y = x(x-1)(x-2)$ のグラフの概形を描きます．

グラフの特徴は以下の通りです．

• 3次関数だから右上がりで始まり，右上がりで終わる．
• $x$ 軸との交点は，$x=0,1,2$ の3つ．

この特徴を確認するだけで，グラフの概形を描くことができます．

グラフの $y \gt 0$ の部分の $x$ の範囲が解になるので，

$0 \lt x \lt 1, \ 2 \lt x$ が解となります．

例2　不等式 $x^4 - 6x^3 + 11x^2 - 6x \geqq 0$ を解け．

まず，左辺を因数分解します．

$\begin{eqnarray*} x^4 - 6x^3 + 11x^2 - 6x \geqq 0\\ x(x^3 -6x^2 +11x -6) \geqq 0\\ x(x-1)(x^2-5x+6) \geqq 0\\ x(x-1)(x-2)(x-3) \geqq 0 \end{eqnarray*}$


次に，多項式関数のグラフの特徴を利用して，
$y = x(x-1)(x-2)(x-3)$ のグラフの概形を描きます．

グラフの特徴は以下の通りです．

• 4次関数だから右下がりで始まり，右上がりで終わる．
• $x$ 軸との交点は，$x=0,1,2,3$ の4つ．

この特徴を確認するだけで，グラフの概形を描くことができます．

グラフの $y \geqq 0$ の部分の $x$ の範囲が解になるので，

$x \leqq 0,\ 1 \leqq x \leqq 2,\ 3 \leqq x$ が解となります．

例3　不等式 $x^5-7x^4+17x^3-17x^2+6x \leqq 0$ を解け．

まず，左辺を因数分解します．

$\begin{eqnarray*} x^5-7x^4+17x^3-17x^2+6x \leqq 0\\ x(x^4-7x^3+17x^2-17x+6) \leqq 0\\ x(x-1)(x^3-6x^2+11x-6) \leqq 0\\ x(x-1)(x-1)(x^2-5x+6) \leqq 0\\ x(x-1)^2(x-2)(x-3) \leqq 0 \end{eqnarray*}$


次に，多項式関数のグラフの特徴を利用して，
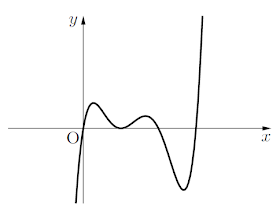
$y = x(x-1)^2(x-2)(x-3)$ のグラフの概形を描きます．

グラフの特徴は以下の通りです．

• 5次関数だから右上がりで始まり，右上がりで終わる．
• $x$ 軸との交点は，$x=0,1,2,3$ の4つ．

この特徴を確認するだけで，グラフの概形を描くことができます．

$x=1$ でグラフが$x$軸と接しているのがポイントです．


グラフの $y \leqq 0$ の部分の $x$ の範囲が解になるので，

$x \leqq 0,\ x=1,\ 2 \leqq x \leqq 3$ が解となります．